
11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
문제
N(2 ≤ N ≤ 100,000)개의 정점으로 이루어진 트리가 주어진다. 트리의 각 정점은 1번부터 N번까지 번호가 매겨져 있으며, 루트는 1번이다.
두 노드의 쌍 M(1 ≤ M ≤ 100,000)개가 주어졌을 때, 두 노드의 가장 가까운 공통 조상이 몇 번인지 출력한다.
풀이
해당 문제는 11437 문제와 동일하게 최소 공통 조상을 찾는 문제지만 데이터가 많아지고 제한 시간이 짧아져 같은 방식으로는 풀 수 없다.
기존의 하나의 부모씩 이동하는 방식으로 풀었을 때는 다음과 같이 시간 초과가 발생한다.

따라서 DP와 결합한 LCA를 사용하여 풀어야한다.
원리는 기존의 하나의 부모씩 거슬러 올라가던것과 달리 2^k 씩 거슬러 올라가 훨씬 빠르게 진행한다.
📌 입력
StringTokenizer st;
for(int i=1; i<N; i++){
st = new StringTokenizer(br.readLine(), " ");
int a= Integer.parseInt(st.nextToken());
int b= Integer.parseInt(st.nextToken());
A[a].add(b);
A[b].add(a);
}기본 LCA와 동일하게 BFS를 사용하기 위해 인접 리스트 형태의 트리 그래프를 만들어준다.
📌parent 배열 만들기
int count =1;
k =0;
while (count <= N){
count <<= 1;
k++;
}
parent = new int[k+1][N+1];- 주어진 노드가 N개라면 2^k 만큼 거슬러 올라갔을 때 N보다 작을 수 밖에 없다.
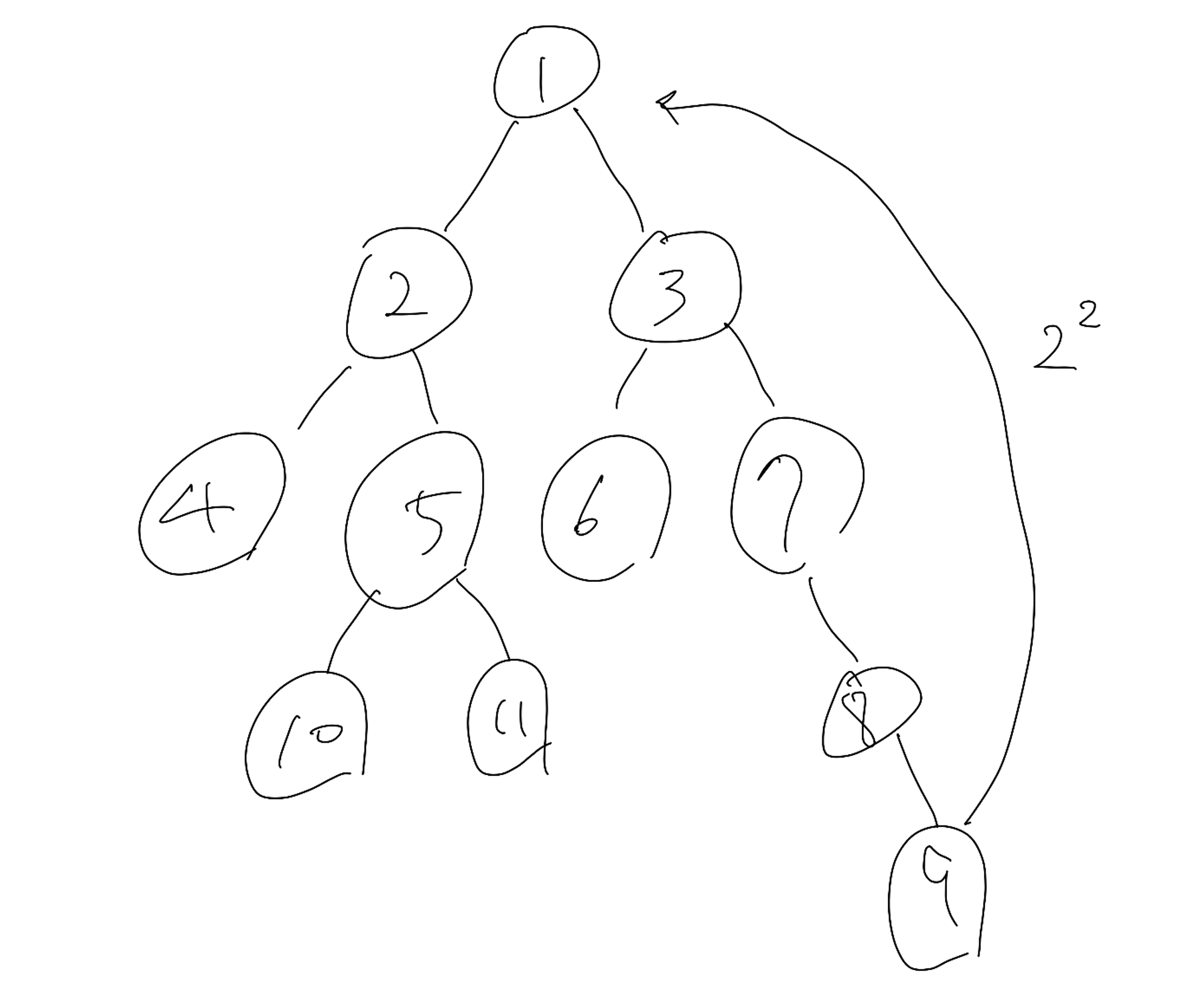
- 위와 같은 트리 그래프가 있을 때, 가장 깊이가 깊은 노드인 9가 아무리 높아 올라가도 2^k ≤ N을 만족하는 k의 최댓값이 된다.
📌 BFS
public static void BFS(int a){
Queue<Integer> q = new LinkedList<>();
q.add(a);
V[a] = true;
while (!q.isEmpty()){
int now = q.poll();
for(int x : A[now]){
if(!V[x]){
q.add(x);
V[x] = true;
depth[x] = depth[now] + 1;
parent[0][x] = now;
}
}
}
}- 루트 노드부터 BFS로 탐색하면서 각 노드의 깊이와 부모 노드를 담아준다.
📌 parent 배열 채우기 (2^k 만큼 거슬러 올라갔을 때의 노드) 점화식
for(int i = 1; i<k; i++){
for(int j=1; j<N+1; j++){
parent[i][j] = parent[i-1][parent[i-1][j]];
}
}- parent 배열은 위와 같은 점화식으로 만들 수 있다. (parent[0][노드번호])가 채워졌을 때)
- 위의 트리 그래프 사진에서는 다음과 같이 구해진다.
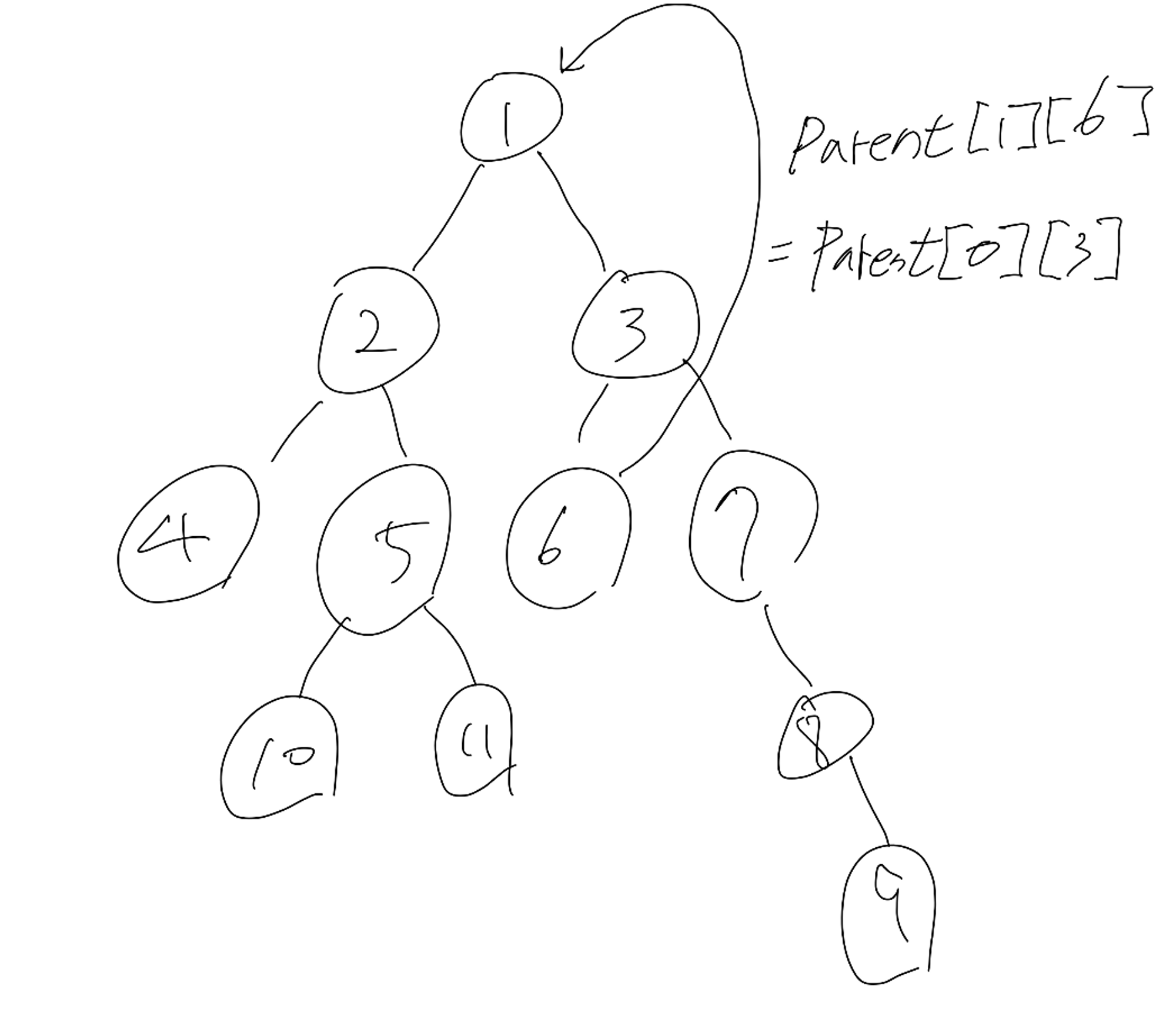
- parent[1][6] = parent[0][parent[0][6]] = parent[0][3] = 1
- 노드 6가 2^1 만큼 거슬러 올라간 노드값 = parent[1][6]
- 노드 6의 부모 노드 = parent[0][6]
- 노드 6의 부모 노드의 부모 노드 = prarent[0][3]
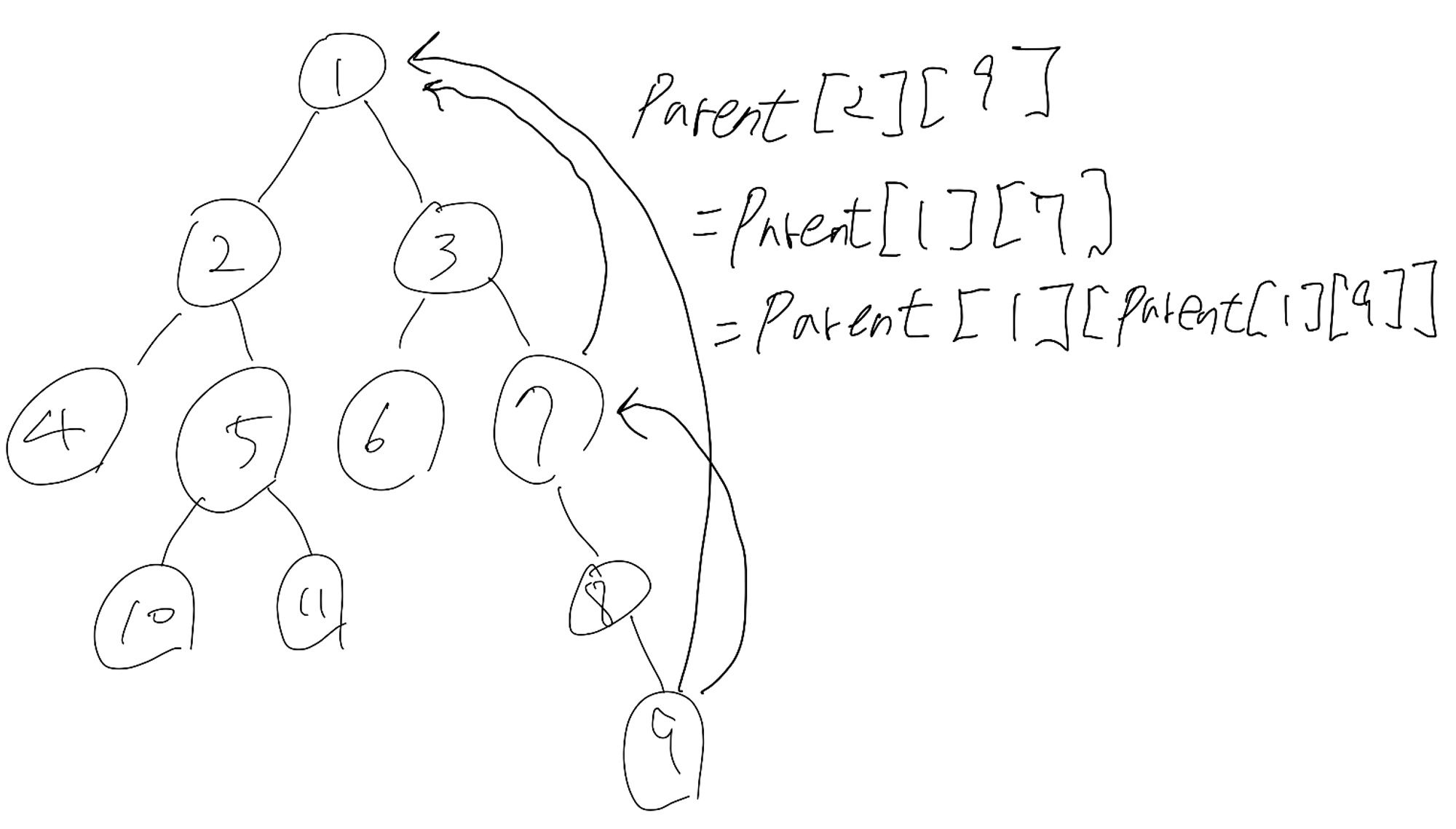
- parent[2][9] = parent[1][parent[1][9]] = parent[1][7] = 1
- 노드 9가 2^2 만큼 거슬러 올라간 노드 값 = prarent[2][9]
- 노드 9가 2^1 만큼 거슬러 올라간 노드 값 = prarent[1][9] = 7
- 노드 9의 2^1 만큼 거슬러 올라간 노드의 2^1 만큼 거슬러 올라간 노드 = parent[1][7]
📌 LCA + DP
public static int LCA(int a, int b){
if(depth[a] > depth[b]){
int temp = b;
b = a;
a = temp;
}
int diff = depth[b] - depth[a];
for(int i=k; i>=0; i--){
if(diff >= Math.pow(2, i) && diff > 0){
b = parent[i][b];
diff = depth[b] - depth[a];
}
}
if(a == b) return a;
for(int i=k; i >= 0; i--){
if(parent[i][a] != parent[i][b]){
a = parent[i][a];
b = parent[i][b];
}
}
return parent[0][a];
}
}- b의 깊이가 항상 더 깊도록 만듭니다.
- b의 깊이와 a의 깊이를 2^k 만큼씩 이동하여 찾습니다.
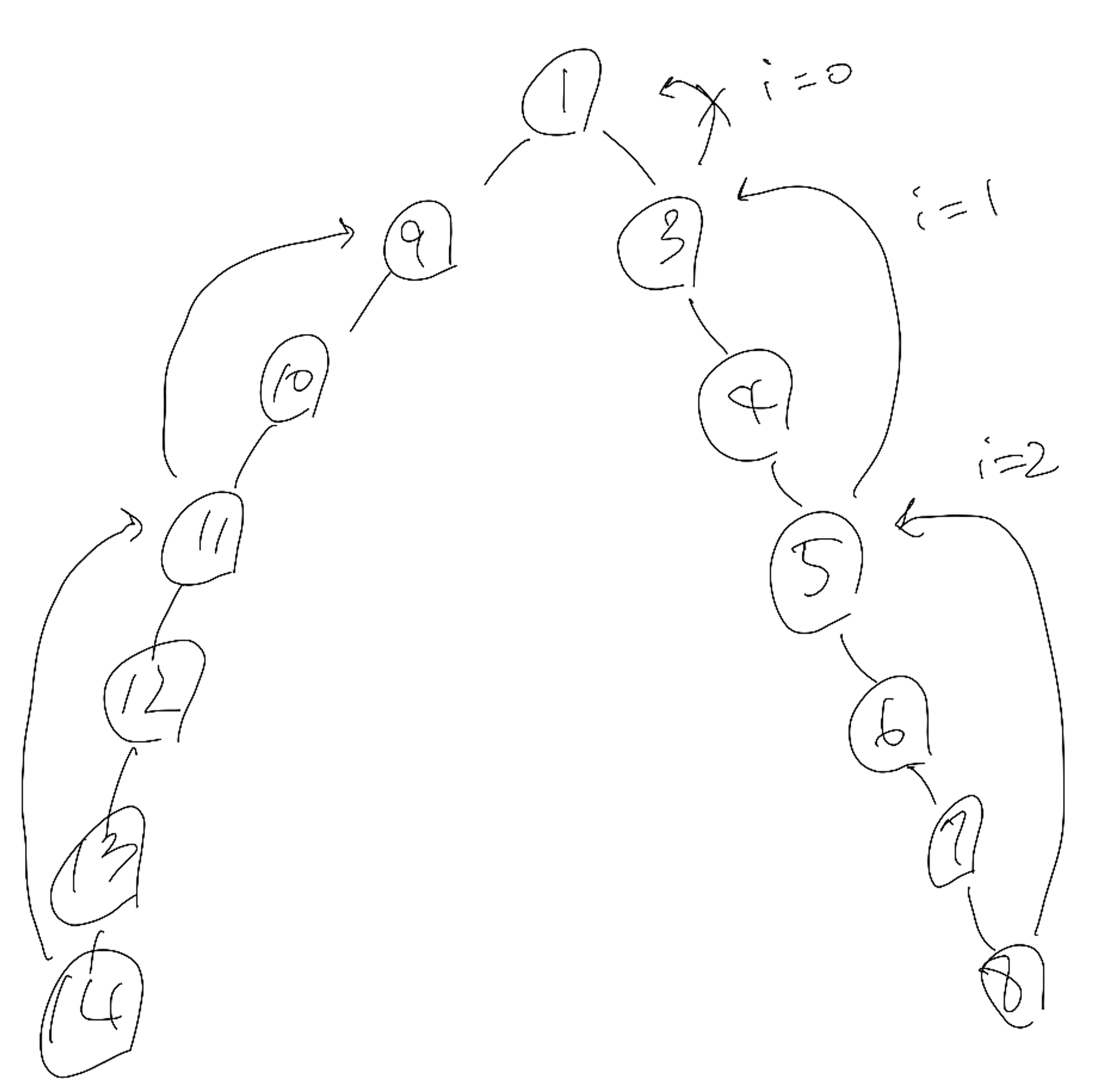
- 만약 두 노드의 깊이 차이가 21일때, 2^k ≤ diff를 만족하는 k의 최댓값인 4를 찾습니다.
- 2^4 = 16만큼 b를 거슬러가고 diff를 갱신합니다. diff = 5
- 다시 2^k ≤ diff 를 만족하는 k의 최댓값인 2를 찾습니다.
- 2^2 = 4 만큼 b를 거슬러가고 diff를 갱신합니다. diff = 1
- 다시 2^k ≤ diff 를 만족하는 k의 최댓값인 0을 찾습니다.
- 2^0 = 1 만큼 b를 거슬러가고 diff를 갱신합니다. diff = 0
- 이제 두 노드의 깊이가 같으므로 종료합니다.
- 만약 여기서 a == b라면 최소 공통 조상을 찾았으므로 반환합니다.
- 두 노드의 깊이를 같이 이동하면서 최소 공통 조상을 찾습니다.
- k의 값을 낮춰가면서 찾는데 2^k를 했을 때 a와 b가 다른 값일 때만 이동합니다.
- 이렇게 이동하는 이유는 a와 b가 같을때, 그 조상이 최소 공통 조상인지 아닌지를 확인할 방법이 없습니다.
- 이렇게 이동한 값의 부모 노드가 바로 공통 조상이 됩니다.
- 2^i 만큼 이동한 값이 다른 노드까지 이동하였으므로 바로 직전노드까지 올라옵니다.
📌 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
class Main {
static int[][] parent;
static boolean[] V;
static ArrayList<Integer>[] A;
static int[] depth;
static int k;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int count =1;
k =0;
while (count <= N){
count <<= 1;
k++;
}
parent = new int[k+1][N+1];
V = new boolean[N+1];
A = new ArrayList[N+1];
depth = new int[N+1];
for(int i=1; i<N+1; i++){
A[i] = new ArrayList<>();
}
StringTokenizer st;
for(int i=1; i<N; i++){
st = new StringTokenizer(br.readLine(), " ");
int a= Integer.parseInt(st.nextToken());
int b= Integer.parseInt(st.nextToken());
A[a].add(b);
A[b].add(a);
}
BFS(1);
for(int i = 1; i<k; i++){
for(int j=1; j<N+1; j++){
parent[i][j] = parent[i-1][parent[i-1][j]];
}
}
int M = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i=0; i<M; i++){
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b= Integer.parseInt(st.nextToken());
sb.append(LCA(a, b)).append("\n");
}
System.out.println(sb);
}
public static void BFS(int a){
Queue<Integer> q = new LinkedList<>();
q.add(a);
V[a] = true;
while (!q.isEmpty()){
int now = q.poll();
for(int x : A[now]){
if(!V[x]){
q.add(x);
V[x] = true;
depth[x] = depth[now] + 1;
parent[0][x] = now;
}
}
}
}
public static int LCA(int a, int b){
if(depth[a] > depth[b]){
int temp = b;
b = a;
a = temp;
}
int diff = depth[b] - depth[a];
for(int i=k; i>=0; i--){
if(diff >= Math.pow(2, i) && diff > 0){
b = parent[i][b];
diff = depth[b] - depth[a];
}
}
if(a == b) return a;
for(int i=k; i >= 0; i--){
if(parent[i][a] != parent[i][b]){
a = parent[i][a];
b = parent[i][b];
}
}
return parent[0][a];
}
}결과

'백준' 카테고리의 다른 글
| [JAVA] 백준 11051 조합 (0) | 2024.03.11 |
|---|---|
| [JAVA] 백준 11050 조합 점화식 (0) | 2024.03.11 |
| [JAVA] 백준 11437 LCA (0) | 2024.03.09 |
| [JAVA] 백준 11505 세그먼트 트리 (1) | 2024.03.08 |
| [JAVA] 백준 10868 세그먼트 트리 (1) | 2024.03.08 |

11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
문제
N(2 ≤ N ≤ 100,000)개의 정점으로 이루어진 트리가 주어진다. 트리의 각 정점은 1번부터 N번까지 번호가 매겨져 있으며, 루트는 1번이다.
두 노드의 쌍 M(1 ≤ M ≤ 100,000)개가 주어졌을 때, 두 노드의 가장 가까운 공통 조상이 몇 번인지 출력한다.
풀이
해당 문제는 11437 문제와 동일하게 최소 공통 조상을 찾는 문제지만 데이터가 많아지고 제한 시간이 짧아져 같은 방식으로는 풀 수 없다.
기존의 하나의 부모씩 이동하는 방식으로 풀었을 때는 다음과 같이 시간 초과가 발생한다.

따라서 DP와 결합한 LCA를 사용하여 풀어야한다.
원리는 기존의 하나의 부모씩 거슬러 올라가던것과 달리 2^k 씩 거슬러 올라가 훨씬 빠르게 진행한다.
📌 입력
StringTokenizer st;
for(int i=1; i<N; i++){
st = new StringTokenizer(br.readLine(), " ");
int a= Integer.parseInt(st.nextToken());
int b= Integer.parseInt(st.nextToken());
A[a].add(b);
A[b].add(a);
}기본 LCA와 동일하게 BFS를 사용하기 위해 인접 리스트 형태의 트리 그래프를 만들어준다.
📌parent 배열 만들기
int count =1;
k =0;
while (count <= N){
count <<= 1;
k++;
}
parent = new int[k+1][N+1];- 주어진 노드가 N개라면 2^k 만큼 거슬러 올라갔을 때 N보다 작을 수 밖에 없다.

- 위와 같은 트리 그래프가 있을 때, 가장 깊이가 깊은 노드인 9가 아무리 높아 올라가도 2^k ≤ N을 만족하는 k의 최댓값이 된다.
📌 BFS
public static void BFS(int a){
Queue<Integer> q = new LinkedList<>();
q.add(a);
V[a] = true;
while (!q.isEmpty()){
int now = q.poll();
for(int x : A[now]){
if(!V[x]){
q.add(x);
V[x] = true;
depth[x] = depth[now] + 1;
parent[0][x] = now;
}
}
}
}- 루트 노드부터 BFS로 탐색하면서 각 노드의 깊이와 부모 노드를 담아준다.
📌 parent 배열 채우기 (2^k 만큼 거슬러 올라갔을 때의 노드) 점화식
for(int i = 1; i<k; i++){
for(int j=1; j<N+1; j++){
parent[i][j] = parent[i-1][parent[i-1][j]];
}
}- parent 배열은 위와 같은 점화식으로 만들 수 있다. (parent[0][노드번호])가 채워졌을 때)
- 위의 트리 그래프 사진에서는 다음과 같이 구해진다.
- parent[1][6] = parent[0][parent[0][6]] = parent[0][3] = 1
- 노드 6가 2^1 만큼 거슬러 올라간 노드값 = parent[1][6]
- 노드 6의 부모 노드 = parent[0][6]
- 노드 6의 부모 노드의 부모 노드 = prarent[0][3]

- parent[2][9] = parent[1][parent[1][9]] = parent[1][7] = 1
- 노드 9가 2^2 만큼 거슬러 올라간 노드 값 = prarent[2][9]
- 노드 9가 2^1 만큼 거슬러 올라간 노드 값 = prarent[1][9] = 7
- 노드 9의 2^1 만큼 거슬러 올라간 노드의 2^1 만큼 거슬러 올라간 노드 = parent[1][7]

📌 LCA + DP
public static int LCA(int a, int b){
if(depth[a] > depth[b]){
int temp = b;
b = a;
a = temp;
}
int diff = depth[b] - depth[a];
for(int i=k; i>=0; i--){
if(diff >= Math.pow(2, i) && diff > 0){
b = parent[i][b];
diff = depth[b] - depth[a];
}
}
if(a == b) return a;
for(int i=k; i >= 0; i--){
if(parent[i][a] != parent[i][b]){
a = parent[i][a];
b = parent[i][b];
}
}
return parent[0][a];
}
}- b의 깊이가 항상 더 깊도록 만듭니다.
- b의 깊이와 a의 깊이를 2^k 만큼씩 이동하여 찾습니다.
- 만약 두 노드의 깊이 차이가 21일때, 2^k ≤ diff를 만족하는 k의 최댓값인 4를 찾습니다.
- 2^4 = 16만큼 b를 거슬러가고 diff를 갱신합니다. diff = 5
- 다시 2^k ≤ diff 를 만족하는 k의 최댓값인 2를 찾습니다.
- 2^2 = 4 만큼 b를 거슬러가고 diff를 갱신합니다. diff = 1
- 다시 2^k ≤ diff 를 만족하는 k의 최댓값인 0을 찾습니다.
- 2^0 = 1 만큼 b를 거슬러가고 diff를 갱신합니다. diff = 0
- 이제 두 노드의 깊이가 같으므로 종료합니다.
- 만약 여기서 a == b라면 최소 공통 조상을 찾았으므로 반환합니다.
- 두 노드의 깊이를 같이 이동하면서 최소 공통 조상을 찾습니다.
- k의 값을 낮춰가면서 찾는데 2^k를 했을 때 a와 b가 다른 값일 때만 이동합니다.
- 이렇게 이동하는 이유는 a와 b가 같을때, 그 조상이 최소 공통 조상인지 아닌지를 확인할 방법이 없습니다.
- 이렇게 이동한 값의 부모 노드가 바로 공통 조상이 됩니다.
- 2^i 만큼 이동한 값이 다른 노드까지 이동하였으므로 바로 직전노드까지 올라옵니다.

📌 전체 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
class Main {
static int[][] parent;
static boolean[] V;
static ArrayList<Integer>[] A;
static int[] depth;
static int k;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int count =1;
k =0;
while (count <= N){
count <<= 1;
k++;
}
parent = new int[k+1][N+1];
V = new boolean[N+1];
A = new ArrayList[N+1];
depth = new int[N+1];
for(int i=1; i<N+1; i++){
A[i] = new ArrayList<>();
}
StringTokenizer st;
for(int i=1; i<N; i++){
st = new StringTokenizer(br.readLine(), " ");
int a= Integer.parseInt(st.nextToken());
int b= Integer.parseInt(st.nextToken());
A[a].add(b);
A[b].add(a);
}
BFS(1);
for(int i = 1; i<k; i++){
for(int j=1; j<N+1; j++){
parent[i][j] = parent[i-1][parent[i-1][j]];
}
}
int M = Integer.parseInt(br.readLine());
StringBuilder sb = new StringBuilder();
for(int i=0; i<M; i++){
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b= Integer.parseInt(st.nextToken());
sb.append(LCA(a, b)).append("\n");
}
System.out.println(sb);
}
public static void BFS(int a){
Queue<Integer> q = new LinkedList<>();
q.add(a);
V[a] = true;
while (!q.isEmpty()){
int now = q.poll();
for(int x : A[now]){
if(!V[x]){
q.add(x);
V[x] = true;
depth[x] = depth[now] + 1;
parent[0][x] = now;
}
}
}
}
public static int LCA(int a, int b){
if(depth[a] > depth[b]){
int temp = b;
b = a;
a = temp;
}
int diff = depth[b] - depth[a];
for(int i=k; i>=0; i--){
if(diff >= Math.pow(2, i) && diff > 0){
b = parent[i][b];
diff = depth[b] - depth[a];
}
}
if(a == b) return a;
for(int i=k; i >= 0; i--){
if(parent[i][a] != parent[i][b]){
a = parent[i][a];
b = parent[i][b];
}
}
return parent[0][a];
}
}결과

'백준' 카테고리의 다른 글
| [JAVA] 백준 11051 조합 (0) | 2024.03.11 |
|---|---|
| [JAVA] 백준 11050 조합 점화식 (0) | 2024.03.11 |
| [JAVA] 백준 11437 LCA (0) | 2024.03.09 |
| [JAVA] 백준 11505 세그먼트 트리 (1) | 2024.03.08 |
| [JAVA] 백준 10868 세그먼트 트리 (1) | 2024.03.08 |
